7482. Торговля
Вдоль трассы Алматы–Тараз расположены n населённых
пунктов, пронумерованных от 1 до n. С наступлением зимы m
неизвестных торговцев привезли из некого аула вязаные шапки и начали продавать
их в этих населённых пунктах.
Торговцы следуют двум принципам:
·
Они не торгуют в одном месте более одного дня.
·
Каждый день они увеличивают цену на шапку.
Более формально, каждый i-й
торговец:
·
Начинает торговлю в населенном пункте li со стартовой ценой xi за одну шапку.
·
Каждый день переходит в соседний населённый пункт: если
накануне он торговал в пункте j, то сегодня торгует в пункте j + 1.
·
Каждый день увеличивает цену на 1: если вчера цена
составляла x, то сегодня она равна x
+ 1.
·
Завершает торговлю в населённом пункте ri (при этом в ri он ещё продаёт).
Для каждого населённого пункта определите максимальную цену
на одну шапку за всю историю торговли.
Вход. В первой строке заданы два целых числа n (1 ≤ n ≤ 3
* 105) и m (1 ≤ m ≤ 3 * 105) –
количество населенных пунктов и количество торговцев соответственно.
Далее следуют m строк, каждая из которых содержит три целых числа li, ri
(1 ≤ li ≤ ri ≤ n) и xi
(1 ≤ xi ≤ 109)
– начальный и
конечный населённые пункты, а также стартовая цена на шапку для i-го
торговца.
Выход. Выведите n целых
чисел, где i-ое число обозначает максимальную цену на одну шапку за всю
историю торговли в i-ом населённом пункте. Если в каком-то пункте торговля не
велась, выведите 0.
|
Пример
входа |
Пример
выхода |
|
5 2 1 3 2 2 4 6 |
2 6 7 8 0 |
РЕШЕНИЕ
структуры данных – дерево отрезков
Анализ алгоритма
Построим дерево
отрезков на
диапазоне [1; n] и
изначально обнулим его. Пусть торговец продавал шапки в населенных пунктах [li; ri], начиная с цены pi.
Разобьем отрезок
[li; ri] на фундаментальные отрезки [lx1; ry1],
[lx2; ry2], …, [lxk;
ryk]. Тогда в вершину, соответствующую отрезку [lxq;
ryq] (1 ≤ q ≤ k), занесем число
pi + сумма длин отрезков
[lxt; ryt], для всех t
< q.
Например, пусть n = 5, и первая торговля охватывает города с
номерами от 2 до 5, начиная с цены 4. Тогда отрезок [2; 5] распадется на
фундаментальные: [2; 2], [3; 3], [4; 5]. После обработки первой операции
дерево отрезков будет выглядеть следующим образом:
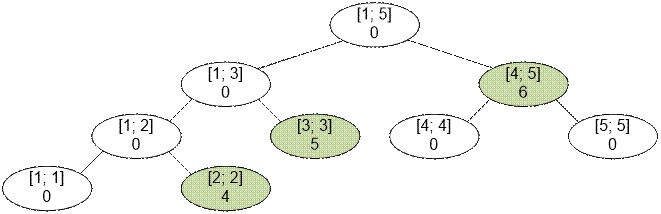
Если
фундаментальный отрезок [a; b] содержит значение p, это означает что:
·
торговец продавал шапки во всех городах от a до b.
·
в городе a шапка продавалась по цене p, в городе
a + 1 по цене p + 1, и так далее, вплоть до города b, где
её цена составляла p + b – a.
Рассмотрим
процедуру обработки
запроса
[left; right] (отрезка, на котором
торговец ведёт торговлю) на диапазоне [lpos; rpos], если начальная цена шапки равна x.
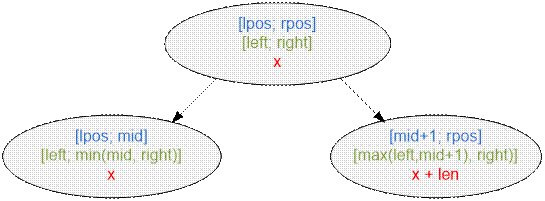
В левом подотрезке торговец будет
продавать шапки в len = min(mid, right) – left + 1 городах,
начиная с цены x. В правом подотрезке первая цена шапки в
городе, куда придёт торговец, составит x + len. Таким образом, на отрезке с номерами [max(left, mid + 1), right] торговля начнётся с цены x + len. Однако
если len < 0 (что возможно, если весь
отрезок запроса находится в правом подотрезке), следует положить len = 0.
Рассмотрим отрезок [a; b],
у которого
есть два подотрезка: [a; m] и [m + 1; b]. Если в городе a торговец продал шапку по цене p, то в городе m + 1 её цена составит p + m + 1 – a.
В процессе обработки
запросов реализуем проталкивание значений, поддерживающее максимум.
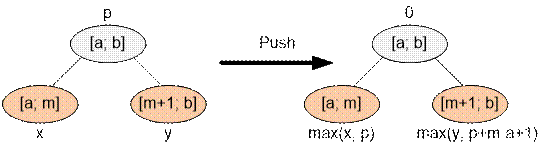
Для вывода
ответа следует пройти по дереву, протолкнуть все значения до листов и
вывести их.
Пример
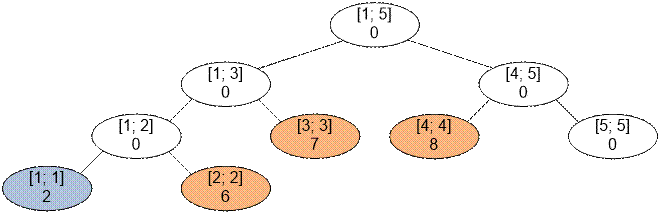
Рассмотрим выполнение двух
запросов, приведённых в примере. Разобьём отрезки запросов на фундаментальные:
·
[1; 3] = [1; 3];
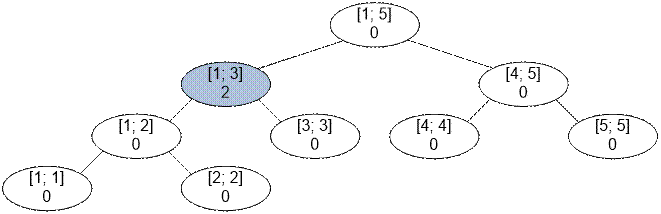
·
[2; 4] = [2; 2] + [3; 3] + [4; 4].
Реализация алгоритма
Объявим массив SegTree для хранения дерева отрезков.
#define MAX 300010
long long
SegTree[4*MAX];
Функция Push выполняет проталкивание значения из вершины v
в ее потомков.
void Push(int v, int lpos, int mid, int rpos)
{
if (SegTree[v])
{
SegTree[2 * v] = max(SegTree[2 * v], SegTree[v]);
SegTree[2 * v + 1] = max(SegTree[2 * v + 1],
SegTree[v] + mid - lpos + 1);
SegTree[v] = 0;
}
}
Функция Update выполняет продажу
шапок на промежутке [left; right], начиная с цены x.
void Update(int v, int lpos, int rpos, int left, int right,
long long x)
{
if (left > right) return;
if ((lpos == left) && (rpos == right))
SegTree[v] = max(SegTree[v], x);
else
{
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos);
int len = min(mid, right) - left + 1;
if (len < 0) len = 0;
Update(2 * v, lpos, mid, left, min(mid, right), x);
Update(2 * v + 1, mid + 1, rpos, max(left, mid + 1),
right, x + len);
}
}
Функция PrintResult проталкивает значения из
внутренних вершин до листьев и выводит итоговое состояние массива.
void PrintResult(int v, int lpos, int rpos)
{
if (lpos == rpos)
printf("%lld ", SegTree[v]);
else
{
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos);
PrintResult(2 * v, lpos, mid);
PrintResult(2 * v + 1, mid + 1, rpos);
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d", &n, &m);
memset(SegTree,0,sizeof(SegTree));
Обрабатываем m запросов.
for(i = 0; i < m; i++)
{
scanf("%d %d
%lld", &l, &r, &x);
Update(1,1,n,l,r,x);
}
Выводим результат.
PrintResult(1,1,n);
printf("\n");